Preguntas PSU Matemática: productos notables

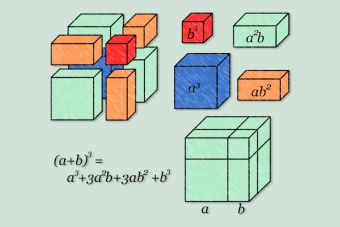
Estos productos son multiplicaciones con expresiones algebraicas, frecuentemente utilizadas en operaciones matemáticas y que corresponden a una fórmula de factorización. Entre los más conocidos se encuentran el cuadrado de binomio y la suma por su diferencia.

Veamos un ejemplo:

Si a ≠ 2, entonces (ax - 2 + a - 2x) / (4 - 4a + a²) =

A) [x + 1] / [2 - a]

B) x / [a - 2]

C) [ax - 1] / a

D) x / [2 - a]

E) [x + 1] / [a – 2]

Como puedes ver, el contenido relacionado con la solución del ejercicio corresponde a factorización y simplificación de expresiones fraccionarias simples.

¿Qué hacer para resolverlo? Necesitas realizar una doble factorización en el numerador teniendo en cuenta que la expresión del denominador corresponde a un cuadrado del binomio. Tras ello, tenemos lo siguiente:

Luego debes factorizar el numerador por (x + 1):

Y por último, debes simplificar por (a - 2):

Por lo tanto, la opción correcta es E).

Si quieres seguir practicando, puedes revisar el link de EducarChile y además consultar algunos de los libros que te sugerimos para que prepares tu PSU.

Imagen CC Wikimedia Commons