Preguntas PSU de Matemáticas: función cuadrática

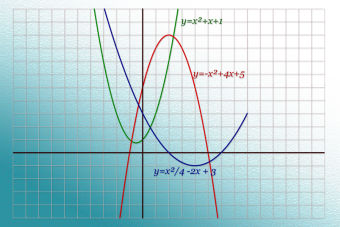
Expresada en la forma f(x) = ax² + bx + c, con "a" distinto a cero, la función cuadrática se representa gráficamente con una parábola cuya orientación cóncava o convexa dependerá del signo que tenga el término cuadrático, es decir, ax².

Veamos un ejercicio del DEMRE:

Si f (x) = x² - x + 3, entonces f (1 - x) es igual a

A) - x² + x

B) x² - x + 3

C) x² + x + 3

D) - x² + x + 3

E) - x² - 3x + 3

Para determinar la alternativa correcta, lo primero es transferir la expresión (1 - x) a la función f(x) = x² - x + 3. Luego resolver el cuadrado de binomio (1 - x)² y reducir términos semejantes.

De ese modo tenemos que:

f (1 - x) = (1 - x)² - (1 - x) + 3

Obteniendo:

1 - 2x + x² - 1 + x + 3

Lo cual nos lleva a:

x² - x + 3

Por lo tanto, la respuesta correcta es la alternativa B). Opción que fue marcada sólo por el 34% de los postulantes.

Y para seguir con álgebra, en este artículo puedes revisar otro ejercicio sobre función cuadrática, en este link puedes ver uno relacionado con expresiones algebraicas fraccionarias y acá puedes ejercitarte con una pregunta referente a ecuación lineal.